1. Matriks A memiliki invers 2 -1 2 1 dan memenuhi A3-c 4+d =c d untuk suatu bilangan real c dan d.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
| d – c | 1 |
A. Kuantitas P lebih besar daripada Q
B. Kuantitas P lebih kecil daripada Q
C. Kuantitas P sama dengan Q
D. Kuantitas P dua kali kuantitas Q
E. Tidak dapat ditentukan hubungan antara kuantitas P dan Q
Jawaban: B
Pembahasan:
![]()
![]()
![]()
![]()
![]()
![]() dan
dan ![]()
![]() maka
maka ![]()
![]()
2. Diberikan matriks ![]() dan
dan ![]() berikut ini :
berikut ini : ![]() Jika
Jika ![]() berturut-turut adalah jumlah entri-entri pada matriks
berturut-turut adalah jumlah entri-entri pada matriks ![]() maka nilai
maka nilai ![]() …
…
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. 2023
Jawaban: E
Pembahasan:
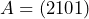
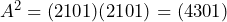
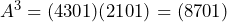
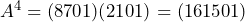
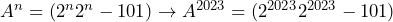
Sehingga
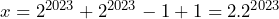
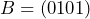
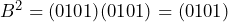
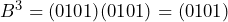
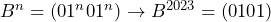
Sehingga
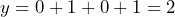
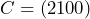
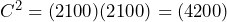
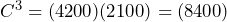
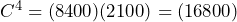
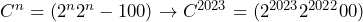
Sehingga
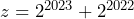
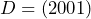
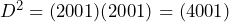
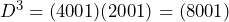
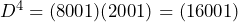
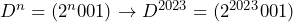
Sehingga
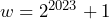
Jadi, ![]()
3. Jika ![]() merupakan matriks yang mempunyai invers dan det
merupakan matriks yang mempunyai invers dan det ![]() = 5 , maka jumlah semua nilai
= 5 , maka jumlah semua nilai ![]() yang mungkin sehingga det
yang mungkin sehingga det ![]() adalah …
adalah …
A. 1
B. 3
C. 8
D. 16
E. 18
Jawaban: B
Pembahasan :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Diketahui matriks ![]() , dan
, dan ![]() adalah matriks berukuran 2×2 yang mempunyai invers. Jika
adalah matriks berukuran 2×2 yang mempunyai invers. Jika ![]() dan
dan ![]() merupakan matriks yang tidak memiliki invers, maka
merupakan matriks yang tidak memiliki invers, maka ![]() …
…
A. -54
B. -38
C. -16
D. 38
E. 54
Jawaban: B
Pembahasan :
Note : tidak memiliki invers ![]()
![]() memiliki invers sehingga det
memiliki invers sehingga det ![]() .
.
![]() tidak memiliki invers, sehingga det
tidak memiliki invers, sehingga det ![]() . Karena
. Karena ![]() maka
maka ![]() . Dengan alasan yang sama, maka
. Dengan alasan yang sama, maka ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5. Diketahui ![]() adalah matriks berordo
adalah matriks berordo ![]() dan
dan ![]() . Jika
. Jika ![]() , maka
, maka ![]() = …
= …
A. -8
B. -4
C. 1
D. ![]()
E. ![]()
Jawaban: D
Pembahasan:
![]()
![]()
![]()
![]()
![]() .
.






